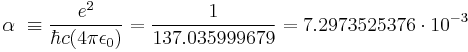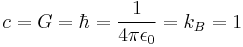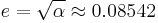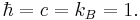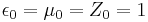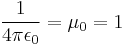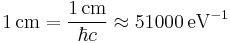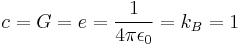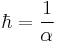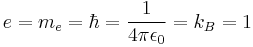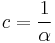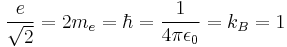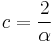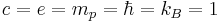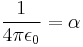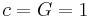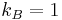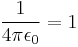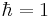Natural units

In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed. A purely natural system of units is defined in such a way that some set of selected universal physical constants are normalized to unity; that is, their numerical values in terms of these units become exactly 1.

1 Introduction
2 Notation and use
3 Advantages and disadvantages
4 Candidate physical constants used in natural unit systems
5 Systems of natural units
6 See also
7 References
8 External links

Introduction

Natural units are intended to elegantly simplify particular algebraic expressions appearing in physical law or to normalize some chosen physical quantities that are properties of universal elementary particles and that may be reasonably believed to be constant. However, what may be believed and forced to be constant in one system of natural units can very well be allowed or even assumed to vary in another natural unit system.

Natural units are natural because the origin of their definition comes only from properties of nature and not from any human construct. Planck units are often, without qualification, called "natural units", when in fact they constitute only one of several systems of natural units, albeit the best known such system. Planck units might be considered unique in that the set of units are not based on properties of any prototype, object, or particle but are solely derived from the properties of free space.

As with other systems of units, the base units of a set of natural units will include definitions and values for length, mass, time, temperature, and electric charge (in lieu of electric current). Some physicists do not recognize temperature as a fundamental physical quantity, since it simply expresses the energy per degree of freedom of a particle, which can be expressed in terms of energy (or mass, length, and time). Virtually every system of natural units normalizes Boltzmann's constant k_B to 1, which can be thought of as simply a way of defining the unit temperature.

In the SI unit system, electric charge is a separate fundamental dimension of physical quantity, but in natural unit systems charge is expressed in terms of the mechanical units of mass, length, and time, similarly to cgs. There are two common ways to relate charge to mass, length, and time: In "rationalized" (or "Heaviside–Lorentz") natural unit systems, Coulomb's law is F=q₁q₂/(4πr²), and in "non-rationalized" (or "Gaussian"), Coulomb's law is F=q₁q₂/r².^[1] Both possibilities are incorporated into different natural unit systems.

Notation and use

Natural units are most commonly used by setting the units to one. For example, many natural unit systems include the equation c = 1 in the unit-system definition, where c is the speed of light. If a velocity v is half the speed of light, then from the equations v = ¹⁄₂c and c = 1, the consequence is v = ¹⁄₂. The equation v = ¹⁄₂ means "the velocity v has the value one-half when measured in Planck units", or "the velocity v is one-half the Planck unit of velocity".

The equation c = 1 can be plugged in anywhere else. For example, Einstein's equation E = mc² can be rewritten in Planck units as E = m. This equation means "The rest-energy of a particle, measured in Planck units of energy, equals the rest-mass of a particle, measured in Planck units of mass."

Advantages and disadvantages

Compared to SI or other unit systems, natural units have both advantages and disadvantages:

Simplified equations: By setting constants to 1, equations containing those constants appear more compact and in some cases may be simpler to understand. For example, the special relativity equation E² = p²c² + m²c⁴ appears somewhat complicated, but the natural units version, E² = p² + m², appears simpler.

Physical interpretation: Natural unit systems automatically incorporate dimensional analysis. For example, in Planck units, the units are defined by properties of quantum mechanics and gravity. Not coincidentally, the Planck unit of length is approximately the length where quantum gravity effects become important. Likewise, atomic units are based on the mass and charge of an electron, and not coincidentally the atomic unit of length is the Bohr radius describing the orbit of the electron in a hydrogen atom.

No prototypes: A prototype is a physical object that defines a unit, such as the International Prototype Kilogram, a certain cylinder whose mass is by definition exactly one kilogram. A prototype definition always has imperfect reproducibility between different places and between different times, and it is an advantage of natural unit systems that they use no prototypes. (They share this advantage with other non-natural unit systems, such as conventional electrical units.)

Less precise measurements: SI units are designed to be used in precision measurements. For example, the second is defined by an atomic transition frequency in cesium atoms, because this transition frequency can be precisely reproduced with atomic clock technology. Natural unit systems are generally not based on quantities that can be precisely reproduced in a lab. Therefore, a quantity measured in natural units can have fewer digits of precision than the same quantity measured in SI. For example, Planck units use the gravitational constant G, which is measurable in a laboratory only to four significant digits.

Greater ambiguity: Consider the equation a = 10¹⁰ in Planck units. If a represents a length, then the equation means a = 1.6×10⁻²⁵ m. If a represents a mass, then the equation means a = 220 kg. Therefore, if the variable a was not clearly defined, then the equation a = 10¹⁰ might be misinterpreted. By contrast, in SI units, the equation would be a = 220 kg, and it would be automatically clear that a represents a mass, not a length or anything else. In fact, natural units are especially useful when this ambiguity is deliberate: For example, in special relativity space and time are so closely related that it can be useful to not specify whether a variable represents a distance or a time.

Candidate physical constants used in natural unit systems

The candidate physical constants to be normalized are chosen from those in the following table. Note that only a smaller subset of the following can be normalized in any one system of units without contradiction in definition (e.g., m_e and m_p cannot both be defined as the unit mass in a single system).

Constant	Symbol	Dimension
Speed of light in vacuum	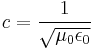$\displaystyle { c } = \frac{1}{\sqrt{\mu_0 \epsilon_0}} \$			L	T⁻¹
Magnetic constant	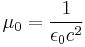$\displaystyle \mu_0 = \frac{1}{\epsilon_0 c^2} \$	Q⁻²	M	L
Electric constant	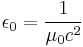$\displaystyle \epsilon_0 = \frac{1}{\mu_0 c^2} \$	Q²	M⁻¹	L⁻³	T²
Coulomb constant	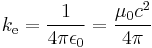$\displaystyle k_\mathrm{e} = \frac{1}{4 \pi \epsilon_0} = \frac{\mu_0 c^2}{4 \pi} \$	Q⁻²	M	L³	T⁻²
Characteristic impedance of free space	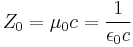$\displaystyle Z_0 = \mu_0 c = \frac{1}{\epsilon_0 c} \$	Q⁻²	M	L²	T⁻¹
Gravitational constant	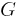${ G } \$		M⁻¹	L³	T⁻²
Planck constant (reduced)	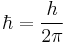$\hbar = \frac{h}{2 \pi}$		M	L²	T⁻¹
Boltzmann constant	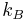${ k_B } \$		M	L²	T⁻²	Θ⁻¹
Elementary charge	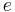${ e } \$	Q
Electron mass	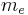${ m_e } \$		M
Proton mass	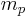${ m_p } \$		M

Judiciously choosing units can only normalize physical constants that have dimension. Dimensionless physical constants cannot take on a different numerical value no matter what system of units is used. One such constant important to physics is the fine-structure constant, α:

$\alpha \ \equiv \frac{e^2}{\hbar c (4 \pi \epsilon_0)} = \frac{1}{137.035999679} = 7.2973525376 \cdot 10^{-3}$

Since α is a fixed dimensionless number not equal to 1, it is not possible to define a system of natural units that will normalize all of the physical constants that comprise α. Any three of the four constants: c, ℏ, e, or 4πε₀, can be normalized (leaving the remaining physical constant to take on a value that is a simple function of α, attesting to the fundamental nature of the fine-structure constant) but not all four.

Systems of natural units

Planck units

Main article: Planck units

Quantity	Expression	Metric value
Length (L)	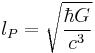$l_P = \sqrt{\frac{\hbar G}{c^3}}$	1.616252×10⁻³⁵ m
Mass (M)	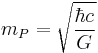$m_P = \sqrt{\frac{\hbar c}{G}}$	2.17644(11)×10⁻⁸ kg
Time (T)	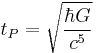$t_P = \sqrt{\frac{\hbar G}{c^5}}$	5.39124 ×10⁻⁴⁴ s
Electric charge (Q)	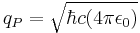$q_P = \sqrt{\hbar c (4 \pi \epsilon_0)}$	1.87554573×10⁻¹⁸ C
Temperature (Θ)	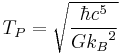$T_P = \sqrt{\frac{\hbar c^5}{G {k_B}^2}}$	1.416785×10³² K

$c = G = \hbar = \frac{1}{4 \pi \epsilon_0} = k_B = 1 \$

$e = \sqrt{\alpha} \approx 0.08542 \$

Planck units are unique among systems of natural units, because they are not defined in terms of properties of any prototype, physical object, or even elementary particle. They only refer to the basic structure of the laws of physics: c and G are part of the structure of spacetime in general relativity, and ℏ captures the relationship between energy and frequency which is at the foundation of quantum mechanics. This makes Planck units particularly useful and common in theories of quantum gravity, including string theory.

Some may consider Planck units to be "more natural" even than other natural unit systems discussed below. For example, some other systems use the mass of an electron as a parameter to be normalized. But the electron is just one of 15 known massive elementary particles, all with different masses, and there is no compelling reason, within fundamental physics, to emphasize the electron mass over some other elementary particle's mass.

"Natural units" (particle physics)

Unit	Metric value	Derivation
1 eV⁻¹ of length	1.97×10⁻⁷ m	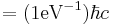$=(1\text{eV}^{-1})\hbar c$
1 eV of mass	1.78×10⁻³⁶ kg	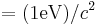$= (1 \text{eV})/c^2$
1 eV⁻¹ of time	6.58×10⁻¹⁶ s	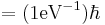$=(1\text{eV}^{-1})\hbar$
1 unit of electric charge (for rationalized)	5.29×10⁻¹⁹ C	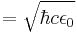$=\sqrt{\hbar c \epsilon_0}$
1 eV of temperature	1.16×10⁴ K	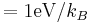$= 1 \text{eV}/k_B$

In particle physics, the phrase "natural units" generally means:^[2]^[3]

$\hbar = c = k_B = 1.$

This is yet not enough information to define a unit system. Next, this equation is almost always supplemented with a definition of charge, from one of two possibilities:

Rationalized (Heaviside–Lorentz units):

${\epsilon_0}={\mu_{0}}={{Z_0}}={1}\,$

Not rationalized (Gaussian units):

$\frac{1}{4\pi\epsilon_0}={\mu_{0}}={1}$

In Heaviside–Lorentz units, there are factors of 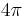$4\pi$ in Coulomb's law and the Biot–Savart law but not in Maxwell's equations; In Gaussian units, it is the reverse. Both systems are used, although Heaviside-Lorentz is more common.^[4] The value of the elementary charge in the two systems is:

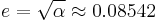$e = \sqrt{\alpha}\approx 0.08542$ (Gaussian).

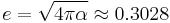$e = \sqrt{4\pi\alpha}\approx 0.3028$ (Lorentz–Heaviside).

Finally, one more unit is needed. Most commonly, electron-volt (eV) is used, despite the fact that this is not a "natural" unit in the sense discussed above. (The SI prefixed multiples of eV are used as well: keV, MeV, GeV, etc.)

With the addition of eV (or any other auxiliary unit), any quantity can be expressed. For example, a distance of 1 cm can be expressed in terms of eV, in natural units, as:^[3]

$1\, \text{cm} = \frac{1\, \text{cm}}{\hbar c} \approx 51000\, \text{eV}^{-1}$

Stoney units

Main article: Stoney units

Quantity	Expression	Metric value
Length (L)	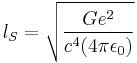$l_S = \sqrt{\frac{G e^2}{c^4 (4 \pi \epsilon_0)}}$	1.38068×10⁻³⁶ m
Mass (M)	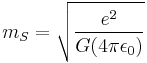$m_S = \sqrt{\frac{e^2}{G (4 \pi \epsilon_0)}}$	1.85921×10⁻⁹ kg
Time (T)	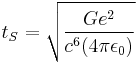$t_S = \sqrt{\frac{G e^2}{c^6 (4 \pi \epsilon_0)}}$	4.60544×10⁻⁴⁵ s
Electric charge (Q)	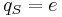$q_S = e \$	1.60218×10⁻¹⁹ C
Temperature (Θ)	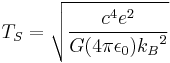$T_S = \sqrt{\frac{c^4 e^2}{G (4 \pi \epsilon_0) {k_B}^2}}$	1.21028×10³¹ K

Stoney units are defined by:

$c = G = e = \frac{1}{4 \pi \epsilon_0} = k_B = 1 \$

$\hbar = \frac{1}{\alpha} \$

where α is the fine-structure constant.

George Johnstone Stoney was the first physicist to introduce the concept of natural units. He presented the idea in a lecture entitled "On the Physical Units of Nature" delivered to the British Association in 1874.^[5] Stoney units differ from Planck units by fixing the elementary charge at 1, instead of Planck's constant (only discovered after Stoney's proposal).

Stoney units are rarely used in modern physics for calculations, but they are of historical interest.

Atomic units

Main article: Atomic units

Quantity	Expression (Hartree atomic units)	Metric value (Hartree atomic units)
Length (L)	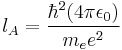$l_A = \frac{\hbar^2 (4 \pi \epsilon_0)}{m_e e^2}$	5.29177×10⁻¹¹ m
Mass (M)	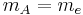$m_A = m_e \$	9.10938×10⁻³¹ kg
Time (T)	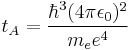$t_A = \frac{\hbar^3 (4 \pi \epsilon_0)^2}{m_e e^4}$	2.41889×10⁻¹⁷ s
Electric charge (Q)	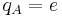$q_A = e \$	1.60218×10⁻¹⁹ C
Temperature (Θ)	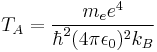$T_A = \frac{m_e e^4}{\hbar^2 (4 \pi \epsilon_0)^2 k_B}$	3.15774×10⁵ K

There are two types of atomic units, closely related: Hartree atomic units:

$e = m_e = \hbar = \frac{1}{4 \pi \epsilon_0} = k_B = 1 \$

$c = \frac{1}{\alpha} \$

Rydberg atomic units:^[6]

$\frac{e}{\sqrt{2}} = 2m_e = \hbar = \frac{1}{4 \pi \epsilon_0} = k_B = 1 \$

$c = \frac{2}{\alpha} \$

These units are designed to simplify atomic and molecular physics and chemistry, especially the hydrogen atom, and are widely used in these fields. The Hartree units were first proposed by Douglas Hartree, and are more common than the Rydberg units.

The units are designed especially to characterize the behavior of an electron in the ground state of a hydrogen atom. For example, using the Hartree convention, in the Bohr model of the hydrogen atom, an electron in the ground state has orbital velocity = 1, orbital radius = 1, angular momentum = 1, ionization energy = ½, etc.

The unit of energy is called the Hartree energy in the Hartree system and the Rydberg energy in the Rydberg system. They differ by a factor of 2. The speed of light is relatively large in atomic units (137 in Hartree or 274 in Rydberg), which comes from the fact that an electron in hydrogen tends to move much slower than the speed of light. The gravitational constant is extremely small in atomic units (around 10⁻⁴⁵), which comes from the fact that the gravitational force between two electrons is far weaker than the Coulomb force. The unit length, m_A, is the Bohr radius, a₀.

Quantum chromodynamics (QCD) system of units

Quantity	Expression	Metric value
Length (L)	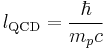$l_{\mathrm{QCD}} = \frac{\hbar}{m_p c}$	2.10308885 × 10⁻¹⁶ m
Mass (M)	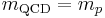$m_{\mathrm{QCD}} = m_p \$	1.67262158 × 10⁻²⁷ kg
Time (T)	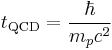$t_{\mathrm{QCD}} = \frac{\hbar}{m_p c^2}$	7.0151493 × 10⁻²⁵ s
Electric charge (Q)	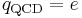$q_{\mathrm{QCD}} = e \$	1.60217646 × 10⁻¹⁹ C
Temperature (Θ)	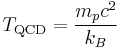$T_{\mathrm{QCD}} = \frac{m_p c^2}{k_B}$	1.0888183 × 10¹³ K

$c = e = m_p = \hbar = k_B = 1 \$

$\frac{1}{4 \pi \epsilon_0} = \alpha$

The electron mass is replaced with that of the proton and the permittivity of free space is not fixed by definition. Strong units are convenient for work in QCD and nuclear physics, where quantum mechanics and relativity are omnipresent and the proton is an object of central interest.^[7]

Geometrized units

Main article: Geometrized unit system

$c = G = 1 \$

The geometrized unit system is not a completely defined or unique system. In this system, the base physical units are chosen so that the speed of light and the gravitational constant are set equal to unity, leaving latitude to also set some other constant such as the Boltzmann constant and Coulomb force constant equal to unity:

$k_B = 1 \$

$\frac{1}{4 \pi \epsilon_0} = 1$

If the reduced Planck constant is also set equal to unity,

$\hbar = 1 \$

then geometrized units are identical to Planck units.

Summary table

Quantity / Symbol	Planck	Stoney	Hartree	Rydberg	Heaviside–Lorentz	Gauss	QCD
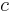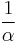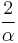Speed of light in vacuum $c \,$	$1 \,$	$1 \,$	$\frac{1}{\alpha} \$	$\frac{2}{\alpha} \$	$1 \,$	$1 \,$	$1 \,$
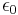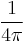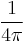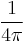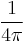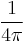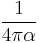Electric constant (vacuum permittivity) $\epsilon_0 \,$	$\frac{1}{4 \pi} \,$	$\frac{1}{4 \pi} \,$	$\frac{1}{4 \pi} \,$	$\frac{1}{4 \pi} \,$	$1 \,$	$\frac{1}{4 \pi} \,$	$\frac{1}{4 \pi \alpha} \,$
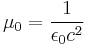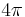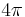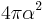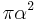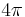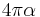Magnetic constant (vacuum permeability) $\mu_0 = \frac{1}{\epsilon_0 c^2} \,$	$4 \pi \,$	$4 \pi \,$	$4 \pi \alpha^2 \,$	$\pi \alpha^2 \,$	$1 \,$	$4 \pi \,$	$4 \pi \alpha \,$
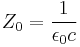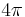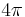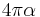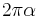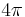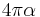Characteristic impedance of vacuum $Z_0 = \frac{1}{\epsilon_0 c} \,$	$4 \pi \,$	$4 \pi \,$	$4 \pi \alpha \,$	$2 \pi \alpha \,$	$1 \,$	$4 \pi \,$	$4 \pi \alpha \,$
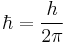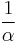Planck's constant (reduced) $\hbar=\frac{h}{2 \pi}$	$1 \,$	$\frac{1}{\alpha} \$	$1 \,$	$1 \,$	$1 \,$	$1 \,$	$1 \,$
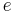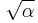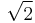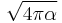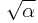Elementary charge $e \,$	$\sqrt{\alpha} \,$	$1 \,$	$1 \,$	$\sqrt{2} \,$	$\sqrt{4\pi\alpha}$	$\sqrt{\alpha}$	$1 \,$
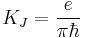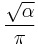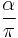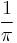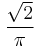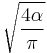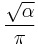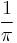Josephson constant $K_J =\frac{e}{\pi \hbar} \,$	$\frac{\sqrt{\alpha}}{\pi} \,$	$\frac{\alpha}{\pi} \,$	$\frac{1}{\pi} \,$	$\frac{\sqrt{2}}{\pi} \,$	$\sqrt{\frac{4\alpha}{\pi}} \,$	$\frac{\sqrt{\alpha}}{\pi} \,$	$\frac{1}{\pi} \,$
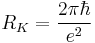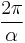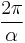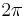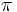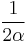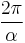von Klitzing constant $R_K =\frac{2 \pi \hbar}{e^2} \,$	$\frac{2\pi}{\alpha} \,$	$\frac{2\pi}{\alpha} \,$	$2\pi \,$	$\pi \,$	$\frac{1}{2\alpha}$	$\frac{2 \pi}{\alpha}$	$2\pi \,$
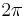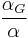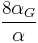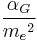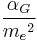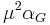Gravitational constant $G \,$	$1 \,$	$1 \,$	$\frac{\alpha_G}{\alpha} \,$	$\frac{8 \alpha_G}{\alpha} \,$	$\frac{\alpha_G}{{m_e}^2} \,$	$\frac{\alpha_G}{{m_e}^2} \,$	$\mu^2 \alpha_G \,$
Boltzmann constant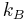 $k_B \,$	$1 \,$	$1 \,$	$1 \,$	$1 \,$	$1 \,$	$1 \,$	$1 \,$
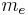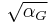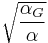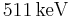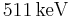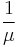Electron mass $m_e \,$	$\sqrt{\alpha_G} \,$	$\sqrt{\frac{\alpha_G}{\alpha}} \,$	$1 \,$	$\frac{1}{2} \,$	$511\, \text{keV}$	$511\, \text{keV}$	$\frac{1}{\mu} \,$

where:

α is the fine-structure constant, 7.2973525376×10⁻³ = (137.035999679)⁻¹,
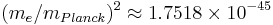α_G is the gravitational coupling constant, $(m_e/m_{Planck})^2 \approx 1.7518\times 10^{-45}$ ,
μ is the proton-to-electron mass ratio, about 1836.15267247.

References

^ Kowalski, Ludwik, 1986, "A Short History of the SI Units in Electricity," The Physics Teacher 24(2): 97-99. Alternate web link (subscription required)
^ Gauge field theories: an introduction with applications, by Guidry, Appendix A
^ ^a ^b An introduction to cosmology and particle physics, by Domínguez-Tenreiro and Quirós, p422
^ http://books.google.com/books?id=12DKsFtFTgYC&pg=PA385 Thermodynamics and statistical mechanics, by Greiner, Neise, Stöcker
^ Ray, T.P. (1981). "Stoney's Fundamental Units". Irish Astronomical Journal 15: 152.
^ Turek, Ilja (1997), Electronic structure of disordered alloys, surfaces and interfaces (illustrated ed.), Springer, pp. 3, ISBN 9780792397984, http://books.google.com/books?id=15wz64DPVqAC&pg=PA3
^ Wilczek, Frank, 2007, "Fundamental Constants," Frank Wilczek web site.

External links

The NIST website (National Institute of Standards and Technology) is a convenient source of data on the commonly recognized constants.
K.A. Tomilin: NATURAL SYSTEMS OF UNITS; To the Centenary Anniversary of the Planck System A comparative overview/tutorial of various systems of natural units having historical use.
Pedagogic Aides to Quantum Field Theory Click on the link for Chap. 2 to find an extensive, simplified introduction to natural units.

Systems of measurement

Metric systems	International System of Units · metre-kilogram-second · centimetre-gram-second · metre-tonne-second · gravitational system

Natural units	Geometric · Planck · Stoney · Lorentz–Heaviside · Atomic · Quantum chromodynamical

Conventional systems	Astronomical · Electrical · Temperature

Customary systems	Avoirdupois · Apothecaries' · British Imperial · Burmese · Canadian · Chinese · Cornish · Danish · Dutch · English · Finnish · French · German · Hindu · Hong Kong · Irish · Japanese · Maltese · Norwegian · Pegu · Polish · Portuguese · Romanian · Russian · Scottish · Spanish · Swedish · Taiwanese · Tatar · Turkish · Troy · United States

Ancient systems	Greek · Roman · Egyptian · Hebrew · Arabic · Mesopotamian · Persian · Indian

Other systems	Non-standard · Mesures usuelles · N-body

Planck's natural units

Base Planck units	Planck time · Planck length · Planck volume · Planck mass · Planck charge · Planck temperature

Derived Planck units	Planck energy · Planck force · Planck power · Planck density · Planck angular frequency · Planck pressure · Planck current · Planck voltage · Planck impedance · Planck momentum

SI units

Base units	Ampere · Candela · Kelvin · Kilogram · Metre · Mole · Second

Derived units	Becquerel · Coulomb · degree Celsius · Farad · Gray · Henry · Hertz · Joule · Katal · Lumen · Lux · Newton · Ohm · Pascal · Radian · Siemens · Sievert · Steradian · Tesla · Volt · Watt · Weber

Accepted for use with SI	Dalton (Atomic mass unit) · Astronomical unit · Day · Decibel · Degree of arc · Electronvolt · Hectare · Hour · Litre · Minute · Minute of arc · Neper · Second of arc · Tonne Atomic units · Natural units

See also	SI prefixes · Systems of measurement · Conversion of units · New SI definitions · History of the metric system

Book:International System of Units · Category:SI base units